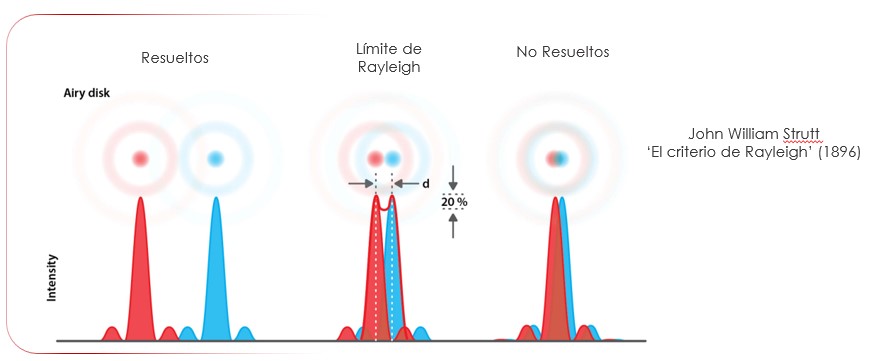
La resolución en microscopía se refiere a la capacidad de un microscopio para distinguir detalles en una muestra, es decir, la distancia mínima a la que dos puntos adyacentes deben estar en una muestra para poder ser resueltos como entidades individuales en la imagen visualizada. Esta característica está influenciada principalmente por la apertura numérica y la longitud de onda de la luz. Ernst Abbe, un físico alemán, estableció la fórmula para definir los límites de difracción del microscopio en 1873. Esta fórmula establece la distancia mínima a la que dos puntos deben estar separados para poder ser resueltos como puntos individuales. La fórmula es d=ʎ/2AN, donde ʎ es la longitud de onda y AN es la apertura numérica de los componentes ópticos. Además, Abbe demostró que la resolución de una imagen aumenta cuando se utiliza longitud de onda corta, medios de inmersión con índice de refracción alto, componentes ópticos de apertura numérica alta o una combinación de estos factores. El límite de difracción de Abbe, que establece la resolución máxima de la microscopía óptica, fue determinado en 1873 y es de aproximadamente 200 nm. Sin embargo, en los últimos años se han desarrollado técnicas de microscopía de superresolución que permiten resolver objetos de tamaño menor que este límite impuesto por difracción, llegando al orden de los 10 nanómetros.
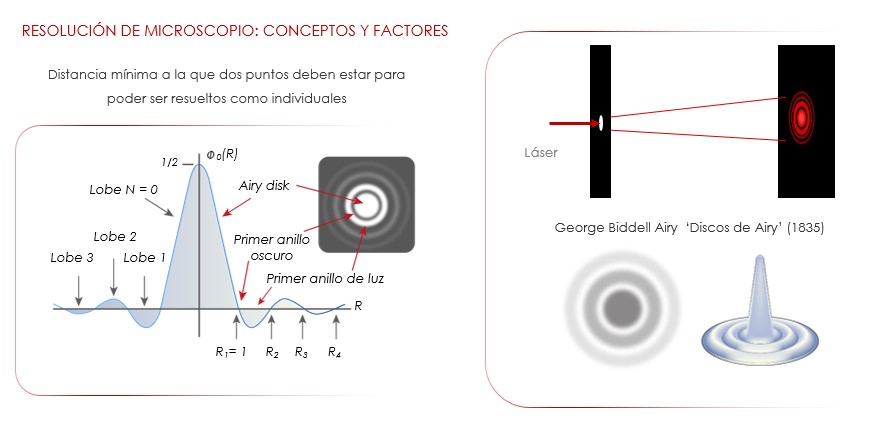

El patrón de difracción descrito en microscopía se produce cuando la luz atraviesa una pequeña apertura con forma circular, lo que produce un patrón de interferencia de regiones iluminadas y oscuras sobre una pantalla alejada. Este patrón de difracción resultante tiene una región central brillante conocida como disco de Airy, rodeado de una serie de anillos concéntricos de intercaladas intensidades (patrón de Airy) que van disminuyendo a medida que se alejan del disco central. El diámetro del disco de Airy está relacionado con la longitud de onda y el tamaño de la abertura por la cual atraviesa, que en el caso de la microscopía sería la apertura numérica del objetivo. La formación de este patrón de difracción se explica por los principios y demostraciones que han permitido definir las características y propiedades de la naturaleza ondulatoria de la luz. Uno de estos principios es el principio de Huygens-Fresnel propuesto por el físico holandés Christian Huygens en 1678, que establece que cada punto de un frente de ondas puede considerarse un foco de ondas secundarias que se propagan en la misma dirección de la perturbación. La velocidad de propagación y frecuencia de estas ondas secundarias es la misma que la de la onda original de donde procede y la superficie tangente (conocida como envolvente) a todas las ondas secundarias en un determinado instante es el siguiente frente de ondas. Otra demostración crucial de la naturaleza ondulatoria de la luz fue el experimento de doble rendija, realizado por Thomas Young en 1802. En este experimento, una fuente de luz coherente, ilumina una placa con dos rendijas paralelas con un tamaño de apertura igual a la longitud de onda que se propaga. Las ondas de luz emergentes de las dos rendijas, interfieren entre sí formando un patrón de regiones claras y oscuras en una pantalla alejada de visualización. Estos principios y demostraciones permitieron explicar los fenómenos ondulatorios relacionados con la propagación de una onda, como por ejemplo la reflexión, la refracción y la difracción.
En la microscopía óptica, el patrón de difracción se produce cuando la luz atraviesa una pequeña apertura con forma circular, lo que produce un patrón de interferencia de regiones iluminadas y oscuras sobre una pantalla alejada. Este patrón de difracción resultante tiene una región central brillante conocida como disco de Airy, rodeado de una serie de anillos concéntricos de intercaladas intensidades (patrón de Airy) que van disminuyendo a medida que se alejan del disco central. La formación de este patrón de difracción se explica por los principios y demostraciones que han permitido definir las características y propiedades de la naturaleza ondulatoria de la luz. En la microscopía, cuando se observa una esfera fluorescente bajo el microscopio, esta va a emitir un frente de onda, el cual es capturado por el objetivo. Este a su vez convierte los rayos en frentes de onda que viajan de forma paralela hasta llegar al siguiente lente, el cual los converge para formar la imagen intermedia en el plano focal. Basado en el principio de Huygens, cada uno de los puntos que componen el frente de onda, actúa como una fuente puntual, que oscila en sincronía con el frente de onda de donde procede. Si dos de estas fuentes de onda puntuales, que componen el frente de onda viajan la misma distancia, al encontrarse van a estar en fase y se generará una interferencia constructiva entre ellas. Esto da como resultado una onda de mayor amplitud (mayor luminosidad), que representa las regiones claras o de mayor luminosidad en patrón de difracción. Por el contrario, si las ondas viajan distancias diferentes, al encontrarse van a estar en desfase, generando una interferencia destructiva y dando como resultado una onda de menor amplitud (menor luminosidad). Esto se traduce a las regiones oscuras del patrón de difracción. Al sumar las interferencias generadas por todas las fuentes puntuales que componen el frente de onda, se formará un patrón de regiones claras y oscuras, conocido como el patrón de difracción o la función dispersión de punto (point spread function (PSF)). Esto quiere decir que una imagen observada a través de un microscopio óptico de luz, es el resultado de la difracción que sufren las ondas al pasar por las pequeñas aperturas de los componentes ópticos y la sumatoria de sus interferencias al converger en el plano focal. Esto da como resultado la función de dispersión de punto.
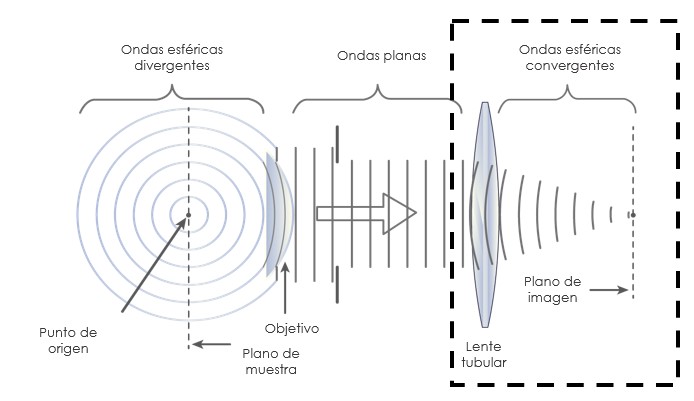
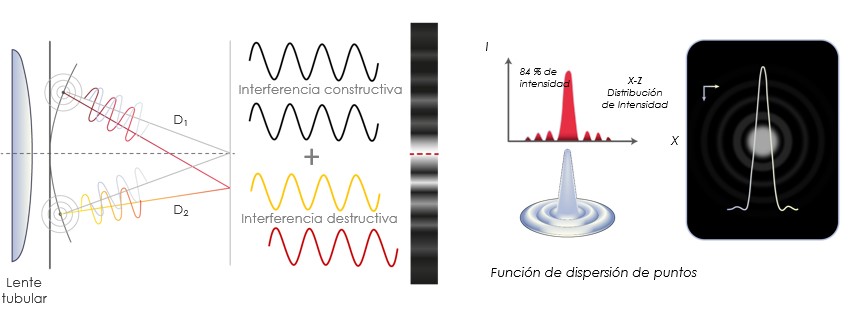
Existen diversos factores que influyen en el tamaño y la definición del patrón de difracción, los cuales tienen un efecto directo sobre la capacidad de resolución. Entre más grande sea la función de dispersión de punto, más difícil será poder resolver dos puntos adyacentes como puntos individuales. Estos factores se revisarán a continuación.
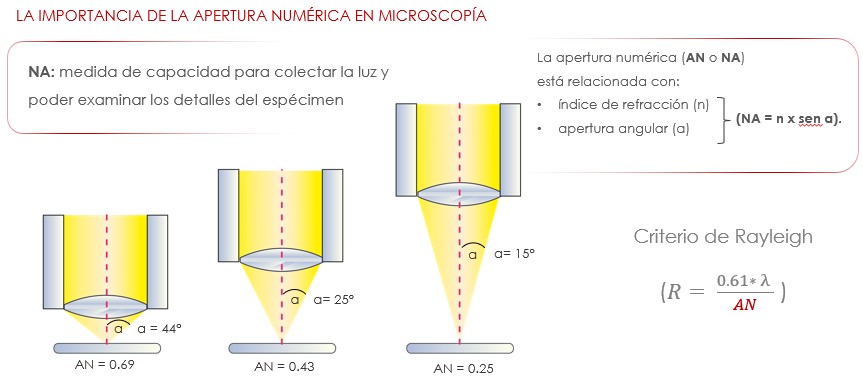
Apertura numérica. Uno de los factores más importantes en cuanto a resolución, es la apertura numérica. Este valor indica la capacidad que tiene un objetivo para captar luz y resolver los detalles finos de la muestra. Se define por la siguiente fórmula; NA = n * (sin α), done n es el índice de refracción del medio entre la lente frontal del objetivo y el cubreobjetos de muestra (valor que oscila entre 1,00 para aire y 1,51 para aceites de inmersión) y alfa (α) es el ángulo de la mitad de la apertura angular del objetivo. En otras palabras, el ángulo formado entre la mitad del cono de iluminación y uno de sus extremos. Entre mayor sea este ángulo, más cantidad de luz es captada por el objetivo y, por lo tanto, más información-resolución se obtendrá de la muestra observada.
Por otro lado, el condensador también produce un cono de luz, el cual proporciona una iluminación homogénea a la muestra. Este cono de luz y su respectiva apertura numérica también juegan un papel fundamental en la resolución, ya que este debe ajustarse correctamente para optimizar el ángulo y por efecto consecuente la intensidad de la luz que ingresa a la lente frontal del objetivo. Por tal razón, cada vez que se cambia un objetivo se debe realizar el ajuste respectivo al condensador (por medio del diafragma de apertura), para proporcionar el cono de luz adecuado que coincida con la apertura numérica del nuevo objetivo.
¿Cómo influye la apertura numérica en la función de dispersión de punto? Cuando se tiene una apertura numérica alta, el frente de onda capturado por dicho objetivo va a estar conformado por una gran cantidad de fuentes puntuales, las cuales van a interferir constructiva y destructivamente, generando un patrón de dispersión de punto angosto y definido. Por el contrario, si el objetivo tiene una apertura numérica baja, el frente de onda capturado por el objetivo, va a estar compuesto por menor cantidad de fuentes puntuales de onda, las cuales, al interferir constructiva y destructivamente, producirán un patrón de dispersión de punto más ancho y menos definido.

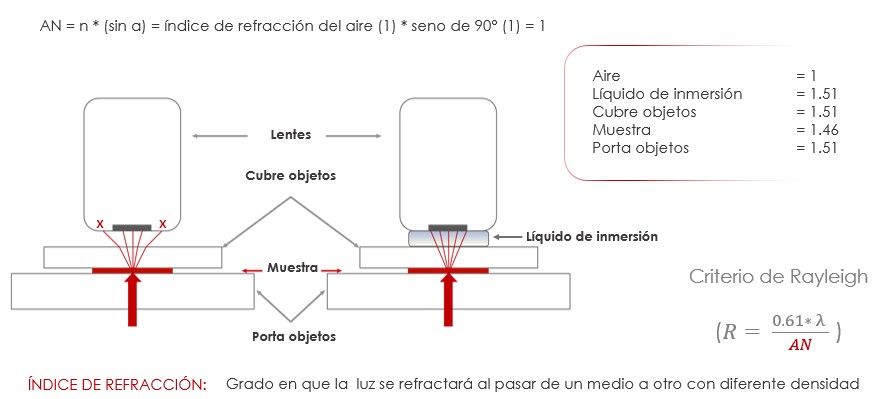
Índice de refracción. Parte de la capacidad que tiene un objetivo para capturar los rayos de luz desviados o refractados de una muestra, depende del medio a través del cual la luz viaja.
Existen objetivos que utilizan el aire como medio a través del cual los rayos de luz deben pasar entre el cubreobjetos y la lente frontal del objetivo, los cuales se denominan objetivos secos. El aire tiene un índice de refracción de 1.0003, el cual es considerablemente más bajo que la mayoría de los líquidos de inmersión (agua: n = 1,33; glicerina: n = 1470, aceites de inmersión promedio: n = 1515). En práctica, la apertura numérica máxima teórica de un objetivo seco, está limitada a 1; como se puede evidenciar en la siguiente ecuación:
AN = n * (sin α) = índice de refracción del aire (1) * seno de 90° (1) = 1
Por tal razón, para lograr aperturas numéricas mayores a 1, es necesario utilizar medios de inmersión. En el caso de un objetivo seco, los rayos que salen de la muestra se refractan en la interfase cubreobjetos-aire, debido a las diferencias entre los índices de refracción haciendo que varios de estos no tengan el ángulo adecuado para lograr ser capturados por el lente frontal del objetivo. Como consecuencia parte de la luz emitida por la muestra se va a perder afectando la resolución de la imagen obtenida y la capacidad e resolver los detalles de la muestra.
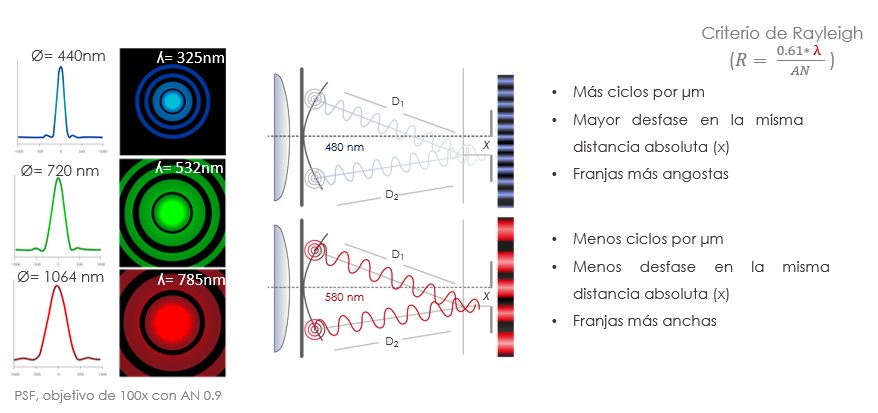
Longitud de onda. La longitud de onda es otro factor de gran importancia en cuanto a la función de dispersión de punto y por ende en la resolución. Entre menor sea la longitud de la onda (ʎ), más ciclos por µm van a haber con mayor desfase por distancia absoluta, produciendo una función de dispersión de punto más angosta y una resolución espacial mejorada. Lo contrario ocurre con las longitudes de onda largas. Esto quiere decir que es más fácil resolver dos puntos adyacentes, cuando se utiliza una longitud de onda corta, por ejemplo, de 325 nm, lo cual formará un patrón de difracción angosto y definido, que cuando se utiliza una longitud de onda larga de por ejemplo 785 nm, lo cual formará un patrón de difracción más grande.